Solution Electrical Numerical 7

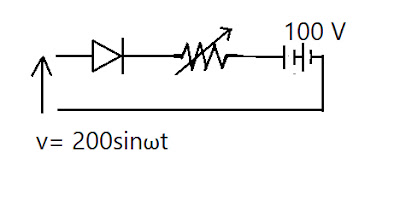
Numerical 7: A battery-charging circuit is shown below in Fig. The forward resistance of the diode can be considered negligible and the reverse resistance infinite. The internal resistance of the battery is negligible. Calculate the necessary value of the variable resistance R so that the battery charging current is 1.0 A.

Solution: It is to be noted that the battery voltage is 100 V. The battery will only be able to charge if a voltage of more than 100 V is applied.

The voltage is given by; V= 200sinωt

Here maximum voltage is 200 Volts. We need to fine the angle between which the voltage is more than 100 V.

100 = 200sinωt

sinωt = 0.5

ωt = $\displaystyle \mathrm{\frac{\pi }{6}\ and\ \frac{5\pi }{6} }$ 

thus the voltage is above 100 V when ωt is between $\displaystyle \mathrm{\frac{\pi }{6}\ and\ \frac{5\pi }{6} }$ 

Now the charging voltage is V-100.

Thus, V-100 = iR

$\displaystyle \mathrm{i = \frac{V-100}{R}}$ 

Here 'i' is the charging current. Average charging current is given by i= 1.0 A

to find the average current we need this equation to be integrated with in the limits $\displaystyle \mathrm{\frac{\pi }{6}\ and\ \frac{5\pi }{6} }$

$\displaystyle \mathrm{1.0 = \frac{1}{2\pi }\int_{\frac{\pi }{6}}^{\frac{5\pi }{6}}\frac{200sin\omega t-100}{R}d(\omega t)}$ 

By solving the above equation we get R = 21.8 Ω