Numerical
22: A ship 100 m long floats at a draught of 6 m and in this condition the immersed cross-sectional areas and water plane areas are as given below. The equivalent base area (Ab) is required because of the fineness of the bottom shell.
Section | AP | 1 | 2 | 3 | 4 | 5 | FP |
Immersed Cross Section area (m^2) | 12 | 30 | 65 | 80 | 70 | 50 | 0 |
Draught (m) | 0 | 0.6 | 1.2 | 2.4 | 3.6 | 4.8 | 6.0 |
Waterplane area (m^2) | A_b | 560 | 720 | 880 | 940 | 1000 | 1030 |
Calculate EACH of the following:
(a) The equivalent base area value Ab.
(b) The longitudinal position of the centre of buoyancy from midships.
(c) The vertical position of the centre of buoyancy above the base.
Solution:
Section | Immersed CSA | SM | Product for volume | Lever | product for moment |
AP | 12 | 1 | 12 | -3 | -36 |
1 | 30 | 4 | 120 | -2 | -240 |
2 | 65 | 2 | 130 | -1 | -130 |
3 | 80 | 4 | 320 | 0 | 0 |
4 | 70 | 2 | 140 | 1 | 140 |
5 | 50 | 4 | 200 | 2 | 400 |
FP | 0 | 1 | 0 | 3 | 0 |
| | | ∑volume=922 | | ∑moment=134 |
h= m
m
(b) The longitudinal position of the centre of buoyancy from midship;
}{\sum(volume)})
LCB= 2.421m (fwd)
Draught | Waterplane area A_w | SM | Product for volume | Lever | product for moment |
0 | A_b | 1/2 | A_b/2 | 0 | 0 |
0.6 | 560 | 4/2 | 1120 | 0.6 | 672 |
1.2 | 720 | 3/2 | 1080 | 1.2 | 1296 |
2.4 | 880 | 4 | 3520 | 2.4 | 8448 |
3.6 | 940 | 2 | 1880 | 3.6 | 6768 |
4.8 | 1000 | 4 | 4000 | 4.8 | 19200 |
6.0 | 1030 | 1 | 1030 | 6.0 | 6180 |
| | | ∑volume=A_b/2+12630 | | ∑moment=42564 |
(a) Equivalent base area value 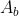
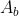 =340.85 m-sq
=340.85 m-sq
(c) The vertical position of center of buoyancy
KB= 3.325m

why is the lever in table 2 is same as the draught?
ReplyDeleteDear Naveen
Deletethanks for posting your question.
The water plane area at the particular draft is given in the question while the water plane area at zero draft is been asked. So it is most likely to use draft for the calculation of moment of volume.
How (h) is taken as 1.2 in second part???
ReplyDeleteDear pirate
Deletethanks for posting your question
Please notice that in the initial three values the draft is having an interval of 0.6.
And after that the interval between drafts is 1.2.
so for compensating the initial difference which is half of the major common interval SM is also used in same manner.
This makes h=1.2 as the common interval.
If still in doubt please let me know.
Formula for h = L/common interval. Then h should be 100/1.2
DeletePlease tell why draught has been used as lever in 2nd table?
ReplyDeleteDear m
Deletethanks for the posting your question.
To find the moment of any area we need a perpendicular distance from reference point to that area.
keeping that in mind draft is used as that 'perpendicular distance'.
why sm is 1/2, 4/2, 1/2 in the second part?
ReplyDeleteDear Ravi
DeleteThe common interval is 1.2 & for that SM is same as we use generally i.e 1, 4, 2, 4, 1.
But whenever the common interval is reduced by some factor, we need to reduce the SM valve by same factor. in this case H is reduced by 1/2 in top three rows., thus SM is also reduced by 1/2.
I Hope now your doubt is clear.
Please feel free to post any query.
sir i feel in case II 3rd sm should be 2x1/2 i.e 1, as we have reduced by 0.5 factor.
ReplyDeleteDear Ravi
DeleteThanks for drawing my attention towards the error.
correction is made.
Follow it like this:
let the common interval 1.2 =h
Then for first three draughts common interval will be h/2.
for first three draughts:
SM with h/2 will be 1,4,1
SM with h will be 1/2, 4/2, 1/2 = 1/2, 2, 1/2
For remaining five draughts SM = 1, 4, 2, 4, 1
(Here we should start from third)
Now finally all together we can write it as
1/2, 2, (1/2+1), 4, 2, 4, 1
or 1/2, 2, 3/2, 4, 2, 4, 1.
Please keep writing your valuable comments.
Why the value of KB h is not multiplied
ReplyDelete