Solution Naval Numerical 25
Numerical
25: A ship of length 120 m displaces 11750 tonne when floating in sea
water of density 1025 kg/m3-cube. The center of gravity is 2m above the
center of buoyancy and the water plane is defined by the following
equidistant half-ordinates given in Table station AP 1, 2, 3, 4, 5, 6, 7
.FP½ breadth (m) 3.3, 6.8, 7.6, 8.1, 8.1, 8.0, 6.6, 2.8, 0. Calculate
EACH of the following: (a) The area of the waterplane; (b) The position
of the centroid of the waterplane from midships; (c) The second moment
of area of the waterplane about a transverse axis through the centroid;
(d) The moment to change trim one centimeter (MCT1cm).The center of
gravity is 2m above the center of buoyancy.
Solution: Given that Length (L) = 120m
Displacement (Δ) =11750 tonne
water density (ρ) = 1025 kg/cu-m
The center of gravity is 2m above the center of buoyancy
Common interval (h) = 120/8 =15
(a) Water plane area (Aw) = 2 x (h/3) x ∑a
Aw = 2x (15/3)×150.7
= 1507 m-sq
(b) Position of centroid of water plane from mid ship = h x ∑m/∑a
=15 x (-65.6/150.7)
= - 6.52
i.e 6.25m aft of the mid-ship
(c)The second moment of area of the waterplane about a transverse axis through the centroid .
We know that the second moment of area of waterplane about the centroid is given bywhere x is the distance of centroid from midships.
Im is the second moment of area of water plane about midships and is given by
thus,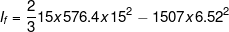
=1296900- 64063.173
= 1232836.82
Displacement (Δ) =11750 tonne
water density (ρ) = 1025 kg/cu-m
The center of gravity is 2m above the center of buoyancy
Common interval (h) = 120/8 =15
(a) Water plane area (Aw) = 2 x (h/3) x ∑a
Aw = 2x (15/3)×150.7
= 1507 m-sq
(b) Position of centroid of water plane from mid ship = h x ∑m/∑a
=15 x (-65.6/150.7)
= - 6.52
i.e 6.25m aft of the mid-ship
(c)The second moment of area of the waterplane about a transverse axis through the centroid .
We know that the second moment of area of waterplane about the centroid is given bywhere x is the distance of centroid from midships.
Im is the second moment of area of water plane about midships and is given by
thus,
=1296900- 64063.173
= 1232836.82
(d) The moment to change trim one centimetre (MCT1cm).
where,
where,
and
thus,MCT1cm = 103.3464tonne-m,

Comments
Post a Comment