Solution Naval Numerical 8
Numerical
8: A box shaped vessel, 50 metres long × 10 metres wide, floats in salt
water on an even keel at a draft of 4 metres. A centre line
longitudinal watertight bulkhead extends from end to end and for the
full depth of the vessel. A compartment amidships on the starboard side
is 15 metres long and contains cargo with permeability 30%. Calculate
the list if this compartment is bilged. KG = 3 metres.
Solution:
Given L = 50m
B = 10m
d = 4m
l = 15m
μ = 30 %.
KG = 3m.
to calculate list:
we know that if a compartment is bilged there is an increase in draught.
which is given by: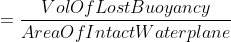
Given that the compartment is having only half the breadth of the ship thus,
Volume of lost Buoyancy can be calculated as:
=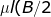d)
= 0.3 x 15 x (10/2) x 4
= 90 cubic-meter
and, The area of intact water plane can be find as:
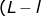B&space;+l(B/2)&space;+l(B/2)(1-\mu&space;))
= (50-15)10 + 15(10/2) + 15x(10/2)(1-0.3)
=350+75+52.2
=477.5 sq-m
Thus, increased in draught = 90/477.5=0.18848m
New draught = 4 + 0.18848 =4.18848m
we know = BMtanθ
= BMtanθ
Solution:
Given L = 50m
B = 10m
d = 4m
l = 15m
μ = 30 %.
KG = 3m.
to calculate list:
we know that if a compartment is bilged there is an increase in draught.
which is given by:
Given that the compartment is having only half the breadth of the ship thus,
Volume of lost Buoyancy can be calculated as:
=
= 0.3 x 15 x (10/2) x 4
= 90 cubic-meter
and, The area of intact water plane can be find as:
= (50-15)10 + 15(10/2) + 15x(10/2)(1-0.3)
=350+75+52.2
=477.5 sq-m
Thus, increased in draught = 90/477.5=0.18848m
New draught = 4 + 0.18848 =4.18848m
we know
Since the BM and GM are assumed to be having a very small difference the above formula can be written as  = GMtanθ
= GMtanθ
but since permiability is given it will be:
where 'μ' = 0.3 (given)
'a' is area of transverse plane of bilged compartment =l xB/2 = 15 x 5 =75 m-sq
'A' is the area of intact water plane i.e 477.5 m-sq (calculated above)
and from the figure we see y = B/4 = 2.5m (it is the distance of centroid of bilged chamber from centre line.
Calculation for GM:-
We know KM= KG+GM
thus, GM= KM-KG
KG = 3m (given)
we still do not know KM, Which we need to calculate,
lets use KM = KB+BM
here KB= draught/2 =4.18848/2 = 2.094m ( New draught is calculated above).
And now BM = I/⛛ ---(i)
Here I is the moment of inertia about the new axis, which can be calculated by using parallel axis theorem.
'H' is the distance of new axis from original axis and 'A' is the area of intact water plane.
Thus H=0.12 m.---(iii)
A=477.5 m-sq---(iv)
Note
in the above expression it is confusing that denominator is different
for both the moment of inertia but it is simply because of the following
facts:
The moment of inertia of a rectangle with respect to an axis passing through its centroid, is given by the following expression:

The moment of inertia of a rectangle with respect to an axis passing through its base, is given by the following expression:
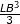
Now from Equation (ii)
substituting values from equation (iii), (iv) and (v)
I = 3979.2 - 477.5 x 0.12 x 0.12 = 3979.2 - 6.876
from equation BM = I/⛛
BM= 1.99m
KM = KB+BM = 2.094+1.99= 4.084 m
GM= KM-KG = 4.084 - 3.0 = 1.084 m
tanθ = 0.12/1.084 =0.1107



Comments
Post a Comment