Solution Naval Numerical 6
Numerical
6: The following data applies to a ship operating on a particular
voyage with a propeller of 6 m diameter having a pitch ratio of 0.95:
propeller speed =1.8 revs/s. Real slip = 34 %, Apparent slip = 7%, Shaft
power =10000 kW, Specific fuel consumption = 0.22 kg/kW-hr. Calculate
EACH of the following: (a) The ship speed in knots; (b) The Taylor wake
fraction; (c) The reduced speed at which the ship should travel in order
to reduce the voyage consumption; (d) The voyage distance if the voyage
takes 3 days longer at the reduced speed; (e) The amount of fuel
required for the voyage at the reduced speed.
Solution:- Given: - D = 6 m
Pitch ratio = 0.95
n = 1.8 rev/s
Real Slip (S) = 34% or 0.34
Apparent slip (Sa)= 7% or 0.07
Shaft power (sp) = 10000 kW
SFC = 0.22 kg/kW-hr
(a) Ship speed (V) = Theoretical speed (Vt) (1 - Sa)
Pitch ratio = Pitch (P)/Diameter(D)
0.95 = P/6
P = 5.7
Vt = P x n x 60 x 60/1852 Knots (n converted to rev/hr)
Vt = 5.7 x 1.8 x 3600/1852
Vt = 19.94 knots
V = 19.94 (1 - 0.07) = 18.547 knots
(b) Taylor’s wake fraction (w) = (V - Va)/V
Va is unknown
Va = Vt (1 - S)
Va = 19.94 (1 - 0.34)
Va = 13.16 knots
w = (18.547-13.16)/18.547
w = 0.298
(c) The reduced speed at which the ship should travel in order to reduce the voyage consumption.
^{3} "\frac{C1}{C2}=\left ( \frac{V1}{V2} \right )^{3}")
We have a reduced consumption to y%.
Original SFC = 0.22kg/kW-hr
Original Consumption = 0.22 x 10000 kg/hr =2200kg/hr.
Reduced consumption = y x 2200/100 = 22y kg/hr
Original ship speed (V1) = 18.547 knots.
To calculate reduced speed.
^{3} "\frac{2200}{22y}=\left ( \frac{18.547}{V2} \right )^{3}")
^\frac{1}{3}Knots "V2 =18.547x\left ( \frac{y}{100}\right )^\frac{1}{3}Knots")
The above expression will give the relation between speed and consumption Let y be 70%, Then V2=16.467 knots.
(d) The voyage distance if the voyage takes 3 days longer at the reduced speed. Let distance be D. Time taken will be distance/speed.
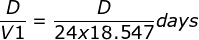
^{1/3}}days "\frac{D}{V2}=\frac{D}{24x18.547x\left ( \frac{y}{100} \right )^{1/3}}days")
New number of days+3 "=\left ( \frac{D}{24x18.547} \right )+3")
Thus,
^{1/3}}&space;\right&space;)=\left&space;(&space;\frac{D}{24x18.547}&space;\right&space;)+3 "\left ( \frac{D}{24x18.547\left ( \frac{y}{100} \right )^{1/3}} \right )=\left ( \frac{D}{24x18.547} \right )+3")
^{1/3}-1} "D=1335.384x\frac{1}{\left ( \frac{y}{100} \right )^{1/3}-1}")
The above expression gives the relation between distance and consumption at reduced speed, with which it takes 3 more days to complete the voyage.
For ex. At 70% consumption (if it takes 3 extra days).
Put y=70 in the above expression, we get D = 10.598.28 nautical miles.
(e) The amount of fuel required for the voyage at the reduced speed.
Daily fuel consumption =0.22 x 10000 x 24 =52800 kg
Original Voyage consumption = No. of days x 52.8 tonne.
x52.8tonne "=\left ( \frac{D}{18.547 x 24} \right )x52.8tonne")
x52.8tonne "=\left ( \frac{10598.28}{18.547 x 24} \right )x52.8tonne")
=1250 tonne
at reduced consumption it is
^{1/3}}&space;\right&space;)x52.8x&space;y "=\left ( \frac{D}{18.547 x 24x\left ( \frac{y}{100} \right )^{1/3}} \right )x52.8x y")
at 70% consumption & D =10598.28 nautical miles, Reduced consumption is
^{1/3}}&space;\right&space;)x52.8x&space;0.7 "=\left ( \frac{10598.28}{18.547 x 24x\left ( \frac{70}{100} \right )^{1/3}} \right )x52.8x 0.7")
=992.18tonne
Solution:- Given: - D = 6 m
Pitch ratio = 0.95
n = 1.8 rev/s
Real Slip (S) = 34% or 0.34
Apparent slip (Sa)= 7% or 0.07
Shaft power (sp) = 10000 kW
SFC = 0.22 kg/kW-hr
(a) Ship speed (V) = Theoretical speed (Vt) (1 - Sa)
Pitch ratio = Pitch (P)/Diameter(D)
0.95 = P/6
P = 5.7
Vt = P x n x 60 x 60/1852 Knots (n converted to rev/hr)
Vt = 5.7 x 1.8 x 3600/1852
Vt = 19.94 knots
V = 19.94 (1 - 0.07) = 18.547 knots
(b) Taylor’s wake fraction (w) = (V - Va)/V
Va is unknown
Va = Vt (1 - S)
Va = 19.94 (1 - 0.34)
Va = 13.16 knots
w = (18.547-13.16)/18.547
w = 0.298
(c) The reduced speed at which the ship should travel in order to reduce the voyage consumption.
We have a reduced consumption to y%.
Original SFC = 0.22kg/kW-hr
Original Consumption = 0.22 x 10000 kg/hr =2200kg/hr.
Reduced consumption = y x 2200/100 = 22y kg/hr
Original ship speed (V1) = 18.547 knots.
To calculate reduced speed.
The above expression will give the relation between speed and consumption Let y be 70%, Then V2=16.467 knots.
(d) The voyage distance if the voyage takes 3 days longer at the reduced speed. Let distance be D. Time taken will be distance/speed.
New number of days
Thus,
The above expression gives the relation between distance and consumption at reduced speed, with which it takes 3 more days to complete the voyage.
For ex. At 70% consumption (if it takes 3 extra days).
Put y=70 in the above expression, we get D = 10.598.28 nautical miles.
(e) The amount of fuel required for the voyage at the reduced speed.
Daily fuel consumption =0.22 x 10000 x 24 =52800 kg
Original Voyage consumption = No. of days x 52.8 tonne.
=1250 tonne
at reduced consumption it is
at 70% consumption & D =10598.28 nautical miles, Reduced consumption is
=992.18tonne
Comments
Post a Comment