Solution Naval Numerical 27

Numerical 27: A ship 100 m long floats at a draught of 6 m and in this condition the immersed cross-sectional areas and water plane areas are as given below.The equivalent base area (Ab) is required because of the fineness of the bottom shell.

 

Section	AP	1	2	3	4	5	FP
Immersed Cross Section area (m^2)	12	30	65	80	70	50	0

 

Draught (m)	0	0.6	1.2	2.4	3.6	4.8	6.0
Waterplane area (m^2)	A_b	560	720	880	940	1000	1030

Calculate EACH of the following: 

(a) The equivalent base area value Ab.

(b) The longitudinal position of the center of buoyancy from midships. 

(c) The vertical position of the centre of buoyancy above the base.

Solution:

 

Section	Immersed CSA	SM	Product for volume	Lever	product for moment
AP	12	1	12	-3	-36
1	30	4	120	-2	-240
2	65	2	130	-1	-130
3	80	4	320	0	0
4	70	2	140	1	140
5	50	4	200	2	400
FP	0	1	0	3	0
			∑volume=922		∑moment=134

h=m

 

 

(b) The longitudinal position of the centre of buoyancy from mid ship;  

 

LCB= 2.421m (fwd)

 

Draught	Water plane area A_w	SM	Product for volume	Lever	product for moment
0	A_b	1/2	A_b/2	0	0
0.6	560	4/2	1120	0.6	672
1.2	720	1/2	1080	1.2	1296
2.4	880	4	3520	2.4	8448
3.6	940	2	1880	3.6	6768
4.8	1000	4	4000	4.8	19200
6.0	1030	1	1030	6.0	6180
			∑volume=A_b/2+12630		∑moment=42564

(a) Equivalent base area value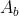

 

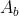=340.85 m-sq

(c) The vertical position of center of buoyancy

 

KB= 3.325m