Answer MET Question 46
Question: A. Explain how the efficiency and regulation of a transformer can
be assessed by open circuit and short circuit test?
B. What is meant by equivalent resistance?
Answer: Open Circuit or No-Lead test
The
purpose of this test is to determine no-load loss or core loss and to
find no load current $\displaystyle \small \mathrm{I_o}$ which is
helpful to find $\displaystyle \small \mathrm{X_o}$ and $\displaystyle
\small \mathrm{R_o}$.
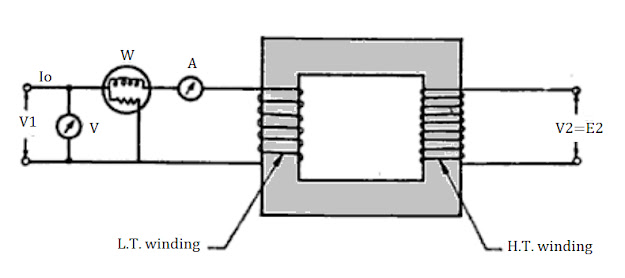
Normal voltage is applied to the primary winding (normally low voltage side) and a wattmeter, voltmeter and ammeter are connected as shown, the secondary being left open.
Normal flux will flow in the core due to normal voltage applied, and wattmeter will record core losses. As the primary no-load current is very small and primary resistance also small, copper loss is negligible in primary winding and nil in secondary being open circuted. Thus, wattmeter reading represents pratically the core loss.
$\displaystyle \small \mathrm{W=V_1I_oCos\phi_o}$
or, $\displaystyle \small \mathrm{Cos\phi_o=\frac{W}{V_1I_o}}$
Magnetizing current = $\displaystyle \small \mathrm{I_\mu =I_osin\phi _o}$ Watt loss component, $\displaystyle \small \mathrm{I_w=I_ocos\phi _o}$
$\displaystyle \small \mathrm{R_o =\frac{V_1}{I_w}}$
$\displaystyle \small \mathrm{X_o =\frac{V_1}{I_\mu }}$
Normal voltage is applied to the primary winding (normally low voltage side) and a wattmeter, voltmeter and ammeter are connected as shown, the secondary being left open.
Normal flux will flow in the core due to normal voltage applied, and wattmeter will record core losses. As the primary no-load current is very small and primary resistance also small, copper loss is negligible in primary winding and nil in secondary being open circuted. Thus, wattmeter reading represents pratically the core loss.
$\displaystyle \small \mathrm{W=V_1I_oCos\phi_o}$
or, $\displaystyle \small \mathrm{Cos\phi_o=\frac{W}{V_1I_o}}$
Magnetizing current = $\displaystyle \small \mathrm{I_\mu =I_osin\phi _o}$ Watt loss component, $\displaystyle \small \mathrm{I_w=I_ocos\phi _o}$
$\displaystyle \small \mathrm{R_o =\frac{V_1}{I_w}}$
$\displaystyle \small \mathrm{X_o =\frac{V_1}{I_\mu }}$
Short circuit test:
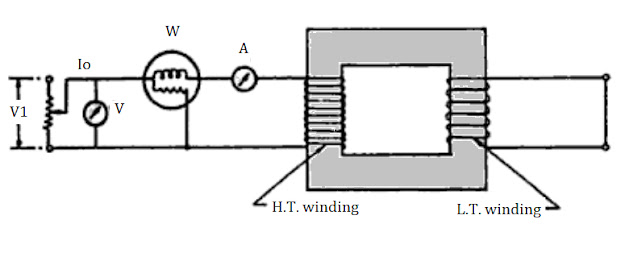
The low voltage side is shorted by a thick conductor and a low voltage is applied
to the primary winding. as shown and the voltage is slowly increased till
full load current flow in both primary and secondary sides. It will be
observed that by applying a very small voltage (of the order of only 5%
of normal voltage) the full load current will flow in both primary and
secondary.
Since the applied voltage is a small % of normal voltage the mutual flux created will also be a small % of normal value, which will lead to a very negligible core loss. Thus the wattmeter reading will represent the entire copper loss for both primary and secondary at full load.
So, $\displaystyle \small \mathrm{W_1 = I_1^2 \times R_{01} }$
$\displaystyle \small \mathrm{Z_{01} = \frac{V_{sc}}{I_1}}$
$\displaystyle \small \mathrm{W_1 = full\ load\ copper\ loss}$
$\displaystyle \small \mathrm{I_1 = Primary\ full\ load\ current}$
$\displaystyle \small \mathrm{R_{01}\ and\ Z_{01} }$ are equivalent resistance and impedance of the equivalent circuit.
Since the applied voltage is a small % of normal voltage the mutual flux created will also be a small % of normal value, which will lead to a very negligible core loss. Thus the wattmeter reading will represent the entire copper loss for both primary and secondary at full load.
So, $\displaystyle \small \mathrm{W_1 = I_1^2 \times R_{01} }$
$\displaystyle \small \mathrm{Z_{01} = \frac{V_{sc}}{I_1}}$
$\displaystyle \small \mathrm{W_1 = full\ load\ copper\ loss}$
$\displaystyle \small \mathrm{I_1 = Primary\ full\ load\ current}$
$\displaystyle \small \mathrm{R_{01}\ and\ Z_{01} }$ are equivalent resistance and impedance of the equivalent circuit.
Efficiency at a power factor cosф lagging.
$\displaystyle \small \mathrm{\eta =\frac{Out\ Put}{In\ Put} = \frac{KVACos\phi}{KVACos\phi + losses} }$
$\displaystyle \small \mathrm{\eta =\frac{Out\ Put}{In\ Put} = \frac{KVACos\phi}{KVACos\phi + W+W_1} }$
Where; W = Core loss & $\displaystyle \small \mathrm{W_1}$ = full load copper loss.
Voltage
Regulation is the ratio of change in secondary terminal voltage from
on-load to full load with the no-load voltage. The drop in voltage takes
place due to internal resistance and leakage reactance of the
transformer winding.
$\displaystyle \small \mathrm{percent\ regn =\frac{V_1-V_2'}{V_1}\times 100 }$
From the vector diagram, it is clear that if angle between $\displaystyle \small \mathrm{V_1\ and\ V_2'}$ is neglected, then
Numerical difference $\displaystyle \small \mathrm{V_1\ -\ V_2'}$ is given by $\displaystyle \small \mathrm{(I_1R_{01}cos\phi + I_1X_{01}sin\phi )}$ for lagging p.f.
thus, $\displaystyle \small \mathrm{Percentage\ regn.=\frac{(I_1R_{01}cos\phi + I_1X_{01}sin\phi )}{V_1}\times 100}$
$\displaystyle \small \mathrm{= V_rcos\phi +V_xSin\phi }$
Where
$\displaystyle \small \mathrm{\frac{I_1R_{01}\times 100}{V_1}=V_r}$ and $\displaystyle \small \mathrm{\frac{I_1X_{01}\times 100}{V_1}=V_x}$
As before, if angle between $\displaystyle \small \mathrm{V_1\ and\ V_2'}$ is not negiligible, then
Numerical difference $\displaystyle \small \mathrm{V_1\ -\ V_2'}$ is given by $\displaystyle \small \mathrm{(I_1R_{01}cos\phi + I_1X_{01}sin\phi )}$ for lagging p.f.
thus, $\displaystyle \small \mathrm{Percentage\ regn.=\frac{(I_1R_{01}cos\phi + I_1X_{01}sin\phi )}{V_1}\times 100}$
$\displaystyle \small \mathrm{= V_rcos\phi +V_xSin\phi }$
Where
$\displaystyle \small \mathrm{\frac{I_1R_{01}\times 100}{V_1}=V_r}$ and $\displaystyle \small \mathrm{\frac{I_1X_{01}\times 100}{V_1}=V_x}$
As before, if angle between $\displaystyle \small \mathrm{V_1\ and\ V_2'}$ is not negiligible, then


Comments
Post a Comment